مثلثی که از روابط بسط نیوتن استفاده کرده و ارایش منظمی از اعداد را  به وجود می آورد.در این پست تاریخچه این مثلث+پروژه آن در زبان پاسکال و توضیح عملکرد برنامه بررسی می شود. 

 

توجه:این برنامه رو من تو وبلاگ انجمن خودمون گذاشتم و این مطلب رو بطور مستقیم از انجمن اینجا قرار میدم

 

مثلث خیام-پاسکال 

مثلثی که از روابط بسط نیوتن استفاده کرده و ارایش منظمی از اعداد را  به وجود می آورد.در این پست تاریخچه این مثلث+پروژه آن در زبان پاسکال و توضیح عملکرد برنامه بررسی می شود. 

 

مثلث خیام-پاسکال 

 

• تاریخچه 

مثلث خیام را در برخی منابع به ندرت «مثلث خیام-پاسکال-نیوتن» نیز می‌گویند. این مثلث در زبان‌های گوناگون نام‌های دیگری نیز دارد در زبان انگلیسی «مثلث پاسکال»، ایتالیایی «مثلث تارتالیا» و در زبان چینی «مثلث یانگ هویی» نام گرفته‌است. در آثار متون سانسکریتِ پینگالا ریاضی‌دان هندی نشانه‌هایی از استفاده از این بسط دیده می‌شود. در همان دوران عمر خیام ریاضی‌دان ایرانی ادعای کشف روشی جبری برای به دست آوردن ضرایب بسط دوجمله‌ای می‌کند. کتاب «مشکلات الحساب»، کتابی که اثبات‌های این ادعا در آن آمده هنوز کشف نشده ولی در آثار طوسی تأثیر گرفته از او ضرایب را تا توان ۱۲ می‌توان دید. بعد از او در قرن ۱۲ میلادی در آثار یانگ هویی ریاضی‌دان چینی، شکل مثلث به چشم می‌خورد. در قرن ۱۶ میلادی ریاضی‌دان ایتالیایی تارتالیا هم از خود این مثلث را به جا گذاشته و پس از یک قرن پاسکال ریاضی‌دان فرانسوی هم دوره با نیوتون روی این بسط و مثلث حسابی آن کار کرد.  

منبع:ویکی پدیا

  

• روابط حاکم 

(a+b)⁰ = 1 (1)
(a+b)¹ = a+b (1,1)
(a+b)² = a²+2ab+b² (1,2,1)
(a+b)³ = a³+3a²b+3ab²+b³ (1,3,3,1)
(a+b)⁴ = a⁴+4a³b²+6a²b²+4a²b³+b⁴ (1,4,6,4,1)
. . .

اعداد داخل پرانتزها، معرف ضریبهای عددی جمله ها در بسط دوجمله ای است.

بلیز پاسکال (Blaise Pascal) فیلسوف و ریاضی دان فرانسوی که کم وبیش با نیوتون همزمان بود، برای تنظیم ضریبهای بسط دوجمله ای، مثلثی درست کرد که امروز به “مثلث حسابی پاسکال” مشهور است. طرح این مثلث برای نخستین بار در سال ۱۶۶۵ میلادی در “رساله مربوط به مثلث حسابی “چاپ شد.مثلث حسابی چنین است:  

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1  

دراین مثلث از سطر سوم به بعد هر عددبرابر با مجموع اعداد بالا و سمت چپ آن در سطر قبل است و بنابراین میتوان آنرا تا هر جا که للازم باشدادامه داد. هرسطر این مثلث ضریبهای بسط دوجمله ای را در یکی از حالتها بدست میدهد بطوری که n همان شماره سطر باشد.  

 

عملکرد برنامه  

در این برنامه از یک ارایه دو بعدی استفاده شده بطوری که یک بعد شامل سطر و یک بعد شامل ستون که همان اعداد هستند را تشکیل می دهند.

 

در مرحله اول برنامه از شما تعداد سطر را درخواست می کند:   

 

بعد از دریافت سطر،عدد در متغیر n ذخیره می شود. 

ابتدا عدد ۱ سطر اول را چاپ می کند.  

سپس در سطر ۲ ارایه ۲و۱ را مقدار “۱” قرار میدهد عدد یک را چاپ کرده و سپس حلقه ستون شروع می شود به این صورت که: 

دو آرایه 1و۱ و 1و۲ را جمع کرده و در ارایه ۲و۲ قرار میدهد.(آرایه ۱و۱ برابر ۱ و ارایه ۱و۲ برابر ۰ است) 

و دوباره مقدار یک را چاپ می کند: 

1
1 1
 

سپس به سطر سوم می رود. 

ابتدا مقدار ۳و۱ را برابر ۱ قرار میدهد.سپس ۱ را چاپ می کند.آرایه ۲و۱ و ۲و۲ را جمع کرده و در ارایه ۳و۲ قرار می دهد(ارایه ۲و۱ برابر ۱ و آرایه ۲و۲ نیز برابر ۱ می باشد) بنابراین ۲ چاپ می شود.

بعد از ان ارایه ۲و۲ و ۲و۳ را جمع کرده و در آرایه ۳و۳ قرار می دهد(ارایه ۲و۲ برابر ۱ و ارایه ۲و۳ برابر . است)پس یک چاپ می شود: 

 

1
1 1
1 2 1 

 

این عملیات تا سطر n بصورت دو حلقه تو در تو ادامه پیدا می کند.  

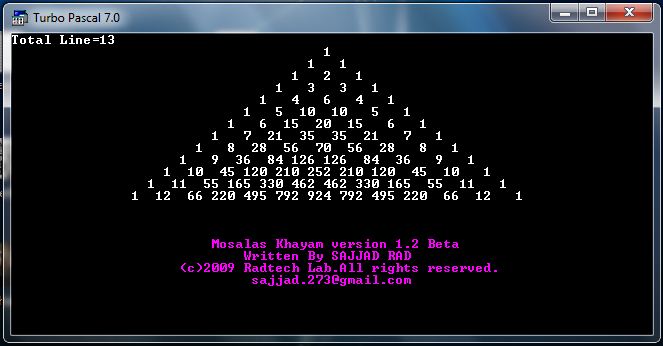
نتیجه برنامه در ۱۳ سطر:   

 

 

 

Persian Young Programmers Team   Pascals Triangle Ver 1.5  Written by SAJJAD RAD  [email protected]

Total Lines:51  Packed by Zip:exe and pas format  password  :  www.myprograms.blogsky.com   Pack Size: 4.6 Kb   Download